- Article
- Published:
An accounting exercise for the shift in life-cycle employment profiles of married women born between 1940 and 1960
Eine Bilanzierung der Verschiebungen der Lebensverlauf-Beschäftigungsprofile von verheirateten Frauen der Jahrgänge zwischen 1940 und 1960
Journal for Labour Market Research volume 46, pages 253–271 (2013)
Abstract
Life-cycle employment profiles of married women born between 1940 and 1960 shifted upwards and became flatter. We calibrate a dynamic life-cycle model of employment decisions of married women to assess the quantitative importance of three competing explanations of the change in employment profiles: the decrease and delay in fertility, the increase in relative wages of women to men, and the decline in child-care costs. We find that the decrease and delay in fertility and the decline in child-care cost affect employment very early in life, while increases in relative wages affect employment increasingly with age. Changes in relative wages, in particular returns to experience, account for the bulk (67 percent) of changes in life-cycle employment of married women.
Zusammenfassung
Lebensverlauf-Beschäftigungsprofile verheirateter Frauen der Jahrgänge zwischen 1940 und 1960 haben sich nach oben verschoben und sind flacher geworden. Wir kalibrieren ein dynamisches Lebenszyklusmodell von Beschäftigungsentscheidungen verheirateter Frauen, um die quantitative Bedeutung von drei konkurrierenden Erklärungen der veränderten Beschäftigungsprofile einzuschätzen: Geburtenrückgang und später eintretende Geburten, Zunahme relativer Löhne von Frauen zu Männern und gesunkene Kosten für Kinderbetreuung. Wir stellen fest, dass Geburtenrückgang und später eintretende Geburten sowie gesunkene Kosten für Kinderbetreuung Beschäftigung in jungen Jahren beeinflussen, wohingegen steigende relative Löhne Beschäftigung im Alter verstärkt beeinflussen. Veränderungen relativer Löhne, vor allem Entlohnung gemäß Erfahrung, stellen den Großteil (67 Prozent) der Veränderungen der Lebenszyklus-Beschäftigungsprofile verheirateter Frauen dar.
1 Introduction
In the United States, as well as in many other developed countries, life-cycle employment profiles of married women born around mid-century changed in a noticeable way. Employment rates of women born in 1940 and earlier are low at childbearing ages (between age 20 to 35) and increase over the life-cycle. Changes in employment across cohorts are not uniform along the life-cycle, however. They are very pronounced at childbearing ages and more modest at later ages. As a result, life-cycle employment profiles of women born in 1960 not only shift upwards but also become much flatter.
In this paper, we build a dynamic life-cycle model of employment decisions of married women to assess the quantitative importance of three competing explanations of the change in life-cycle employment profiles: the decrease and delay in fertility, the increase in relative wages of women to men, and the decline in child-care costs. The incentives at work are not new. First, because child-rearing is intensive in women’s time, employment at childbearing ages increases as fertility is reduced. Second, postponing fertility allows women to reach childbearing ages with a higher stock of accumulated work experience, thereby increasing their incentives to remain employed when having children. Finally, either an increase in women’s wages relative to men or a decline in the cost of child-care makes working more attractive at childbearing ages, which feeds back on employment decisions later on in life because of experience accumulation.
After calibrating the model to the life-cycle facts characterizing the 1940 cohort, we show that the decrease and delay in fertility (both taken as exogenous here) and the decline in child-care cost affect employment very early in life, while increases in relative wages affect employment increasingly with age. Assuming that the three forces account for 100 percent of the shift in life-cycle employment profiles, we find that changes in women’s wages (in particular, returns to experience) account for 67 percent of the increase, versus 21 percent for cost of child-care, and 9 percent for fertility patterns (the residual term is equal to 2 percent). The effects of the decrease and the delay in fertility partly offset each other. Here is how. Employment rates tend to increase following a decrease in fertility since participation rates decrease with the number of children. However, a delay in the timing of births increases the number of (costly) young children in the household at later ages and therefore tends to decrease participation.
Our calibration procedure is new, as dynamic life-cycle models of employment decisions of married women are often estimated using maximum likelihood techniques (e.g., Eckstein and Wolpin 1989; Van der Klaauw 1996, or Francesconi 2002, to name only a few papers). Maximum likelihood is a more refined statistical procedure since it takes into account higher order moments, while we only match the average employment along the life-cycle.Footnote 1 Since large panel data sets are not available yet for the early cohorts we consider, we use a sequence of cross-sectional data from the Current Population Survey (CPS) from 1962 to 2004. Hence, we do not have all the information necessary to perform the maximum likelihood (i.e., conditional means and variances). We believe that calibrating the model is appropriate for the question at hand and find that it yields surprisingly good results. We obtain a very tight fit not only for the entire life-cycle employment profile of the 1940 cohort, but also for the employment by number of children at various ages. Moreover, we conduct sensitivity analysis to assess the robustness of our choice of parameter values.
The contribution of our accounting exercise is clear. Three influential papers have stressed the importance of changes in the pure gender wage gap Jones et al. 2003, changes in returns to experience (Olivetti 2006), and changes in child-care costs relative to life-time earnings (Attanasio et al. 2008) to account for changes in women’s labor supply either over time or across cohorts. Since our model nests these three potential explanations and adds another one (the decrease and delay in fertility), we can assess the quantitative importance of each of these forces separately. We find that they affect employment of women in distinct age groups differently and that changes in returns to experience have the largest impact on women’s employment. Moreover, we show that a careful modeling of the distributions for number and timing of births is fruitful. First, it allows us to match the entire life-cycle employment of married women born in 1940. Second, once we control for changes in fertility patterns, exogenous changes in women’s wages and cost of children that are needed to match changes in employment across cohorts are smaller in magnitude or larger but with a smaller effect on female labor supply compared to the ones found in Jones et al. (2003) for the gender wage gap, Olivetti (2006) for returns to experience, and Attanasio et al. (2008) for decreases in the cost of child-care.
Numerous other explanations for the increase in employment of married women, either over time or across cohorts, have been proposed. These include falling prices of home appliances (Greenwood et al. 2005), changes in the perceived value of marriage (Caucutt et al. 2002), the introduction of the pill (Goldin and Katz 2002), changes in social norms (Fernandez et al. 2004), tax reform (Bar and Leukhina 2009), or gender-biased technological change favoring women (Galor and Weil 1996), to name only a few. These papers are certainly important. However, it is virtually impossible, let alone desirable, to include all of the aforementioned forces into one single model. To perform our accounting exercise, we chose the ones which could be modeled without too much controversy and seemed the most likely to influence women’s employment decisions at childbearing ages.
A note on education is in order. For both cohorts of women (born in 1940 and 1960), college educated women have higher participation rates than women with a high school degree. Hence, part of the increase in the average participation rate of married women can be attributed to the compositional shift from high school to college education. However, in the Appendix, we show that increases in employment rates are also the largest at childbearing ages conditional on education levels. We then describe the total number of children ever born and age at birth of first child for women with different education. We find similar patterns by education as for the average, i.e. fertility levels declined and women have their first child later. As a result, the increase in the fraction of women with a college degree can only account for a fraction of the average increase in women’s employment across cohorts. In this paper, we concentrate on the shift of the curve, rather than underlying compositional changes.
The paper is built as follows. In Sect. 2, we present evidence for the change in life-cycle patterns of employment and fertility for two cohorts of married women born in the United States in 1940 and 1960. In Sect. 3, we describe a dynamic life-cycle model of employment decisions of married women with experience accumulation. In Sect. 4, we explain our procedure for the calibration of the model. In Sect. 5, we perform the accounting exercise and, finally, we provide some concluding remarks in Sect. 6.
2 Data
We use data from the Current Population Survey (CPS) for the survey years 1964–2003 and from the decennial Census for the survey years 1970–2000 to describe the life-cycle patterns of employment and fertility for two cohorts of married women born in the United States in 1940 and 1960.Footnote 2
2.1 Employment
In Fig. 1, we present the average employment by age for married women born in 1940 and 1960. We count as employed, any woman who was at work during the week preceding the interview or has a job but was not at work last week due to illness, vacations, etc. We pool data for women born within a three year interval (i.e., women born from 1939 to 1941 for the 1940 cohort and from 1959 to 1961 for the 1960 cohort) for the number of observations to be large enough at each age and we present both raw data as well as smoothed life-cycle employment profiles. Employment rates for women are low during childbearing ages (between age 20 to 35) and progressively increase over the life-cycle. Changes in employment rates across cohorts, however, differ in magnitudes along the life-cycle and are the largest at childbearing ages. Employment rates increased on average by 24 percentage points between age 20 and 35, compared to only 11 percentage points between age 36 and 50 (see Table 1). This fact is the focus of our analysis.
2.2 Fertility
We use Census data for the years between 1980 and 2000 to describe the distributions for the total number of children ever born and the age of mother at birth of first child of married women born in 1940 and 1960. We consider married women at age 40, assuming that fertility is close to completion at that age, and record the fraction with 0,1,…,4+ children, where 4+ denotes married women with at least 4 children. On average, women born in 1940 had 2.6 children by age 40, while those born in 1960 had 1.9 (see Table 2). Moreover, the decrease in the total number of children ever born mainly occurred from a redistribution of mass away from 3 and 4 children towards 0, 1, and 2 children (see Fig. 2).
The age at birth of first child is not directly reported as part of the Census data. We use the age of the mother and the age of oldest child in the household to calculate a proxy for age of mother at birth of first child. For each number of children ever born, f∈{0,1,2,3,4+}, we record the fraction of women who have their first child at age a∈{20,21,…,40}. On average, women born in 1940 had their first child at age 23, while those born in 1960 had their first child three and a half years later (see Table 2). The increase in the average age at birth of first child can be decomposed into two components: first, for any given level of completed fertility the average age increased across cohorts (see Fig. 3); second, women who have many children tend to have their first child early and the fraction of women with 3 and 4 children (having children early) decreased while the fraction of women with 0, 1, and 2 children (having children late) increased (see Figs. 2 and 3).
2.3 Crossing employment and fertility
To understand how changes in the total number of children ever born and the age of mother at birth of first child affect employment rates along the life-cycle, we describe the employment decisions by number of children in the household at age 30 and 40 for our two cohorts (see Figs. 4 and 5).
Focusing on the behavior of the 1940 cohort, it is clear that women’s employment at age 30 is decreasing in the number of children in the household and that this effect is stronger for the first child. Note from Table 2 that the total number of children ever born decreased from 2.6 to 1.9 children per woman. Based on this fact alone, women’s employment can increase across cohorts, due to a movement along a downward sloping curve. However, employment at age 30 also increased across cohorts for any given number of children. As childbirth is postponed, the fraction of women who used to have 2,3,4+ children at age 30 decreased and employment decreases with the number of children. Moreover, women born in 1960 are also more likely to have accumulated more work experience before childbearing, and therefore, are less likely to drop out of labor markets when having children. As a result, changes in the timing of births can account for the upward shift of the employment curve across cohorts. To assess the latter effect, a model of employment and experience accumulation is needed.
Finally, we present employment rates by total number of children ever born for married women at age 40 in Fig. 5.Footnote 3 We find that, at least qualitatively, employment at age 40 also decreases with the number of children and that it increased across cohorts for any number of children. However, quantitatively, the impact of children on employment is not as strong as the one at age 30, as the differential in employment rates between women with no children and women with 4 children is much smaller than the same difference for women at age 30.
3 A life-cycle model
In this section, we build the aforementioned economic mechanisms into a life-cycle model of employment decisions of married women with heterogeneous agents and experience accumulation. Our model is close to Eckstein and Wolpin (1989).
3.1 Household’s maximization problem
Demographics and fertility
Men and women live with certainty for T periods and women are fertile for T f <T periods. Fertility is exogenous and women differ in the total number of children they have in a life-time, f∈{0,1,…,f max}, and in the age at which they have their first child, a.Footnote 4 We fix the spacing of births to 2 years, so that the timing of all births is fully characterized by women’s permanent type, (f,a): women of type f≥1 can have their first child by age T f −2(f−1) at the latest. Women know their type with certainty at the beginning of their life.
Preferences
Households derive utility from market consumption, c t , and leisure time, l t . We assume that the period-t utility, U(c t ,l t ), is twice-continuously differentiable, increasing, and concave in both arguments, c t and l t .
Dynamic optimization problem
We model employment decisions of married women as a discrete choice, e t ∈{0,1}.Footnote 5 At each age t∈{1,2,…,T}, women receive a wage offer, w t (h t ,ϵ t ), which depends positively on work experience accumulated up to period t, h t , and a contemporaneous productivity shock, ϵ t . Women who accept the wage offer, i.e. e t =1, devote a fixed fraction of her time, t w ∈(0,1), to market activities and gain an additional year of work experience. The law of motion of work experience and women’s wage offers are given by:
and
where ϵ t is normally distributed with mean 0 and standard deviation, \(\sigma_{\epsilon}^{2}\), and is i.i.d. over time.Footnote 6 We do not model joint participation decisions between husbands and wives. Men work with certainty in each period and their (deterministic) wage in period t is equal to w mt .Footnote 7 Given the time discount factor, δ∈(0,1), women of type (f,a) choose employment, e t , to maximize the expected discounted utility, \(E_{t-1}\sum_{s=t}^{T}\delta^{s-t}U(c_{s},l_{s})\), subject to a sequence of budget and time constraints and the law of motion for work experience. In period t, the budget and time constraints are given by:

where the time-invariant functions, g(⋅,⋅,⋅) and t(⋅,⋅,⋅), denote the goods and time cost of children, respectively. Notice that we model the costs of children carefully, allowing them to depend on the age of children and women’s participation choices. Following the work of Hotz and Miller (1988), we assume that both functions are increasing in the number of children and decreasing in age of children. On the other hand, goods costs increase with participation, while time costs decrease. This reflects the necessity of some sort of (paid) child-care when the woman works.
Our model abstracts from several important features. First, households cannot borrow or lend, implying that the only way to smooth consumption over the life-cycle is through women’s labor supply.Footnote 8
Second, there is no depreciation in skills when women drop out of labor markets and only the stock of accumulated work experience, as opposed to the entire history of past employment decisions, matters to determine the average wage offers. Although these assumptions considerably reduce the dimension for the state space, Altug and Miller (1998) show that recent work experience is more valuable than distant one to determine women’s wage offers.
Third, there are no permanent differences in women’s market ability (fixed effects). Francesconi (2002) and Heckman and Walker (1990) find that high ability women are more likely to postpone fertility. Similarly, Van der Klaauw (1996) and Caucutt et al. (2002) show that women with high market ability tend to postpone marriage (they wait for a suitable match), which, in turn, influences the age at which they have their first child and their employment decisions along the life-cycle. We briefly address this issue in Sect. 4.2.
Also, we assume that women’s wage shocks are i.i.d. over time. The i.i.d. assumption considerably reduces the dimension of the state space since we only need to keep track of the current productivity shock, the permanent fertility types, and the number of years of experience.Footnote 9 In addition, since work experience is endogenous, women’s wages become endogenously serially correlated across periods even though productivity shocks are i.i.d.Footnote 10
Finally, note that husband’s wages are deterministic. One reason for women born in 1960 to be more attached to the labor market than women born in 1940 could be an increase in male income risk (see Sommer 2012). We abstract from this mechanism to focus on the effect of relative wage changes, changes in the price of child-care and, most importantly, the decrease and delay in fertility on female labor force participation.
3.2 Dynamic program
We denote by V t (h,ϵ;θ) the maximum expected life-time utility discounted back to period t for women of type θ=(f,a), who are in state (h,ϵ). The household maximization problem can be formulated as a dynamic program, whose Bellman equation is given by:

subject to the law of motion (1), the earnings equation (2), and the budget and time constraints (3). Plugging the budget and time constraints into women’s utility, we define the function, \(W^{e_{t}}_{t}(h,\theta,\epsilon)\), as:

Notice that \(W^{0}_{t}\) is independent of ϵ t , while \(W^{1}_{t}\) is an increasing concave function of ϵ t . As a result, there exists a reservation productivity shock, ϵ ∗(h,β i ,θ), such that women are indifferent between working and not-working, i.e. \(W^{0}_{t}(h,\theta )=W^{1}_{t}(h,\theta,\epsilon^{\ast}_{t})\), and women work if and only if \(\epsilon_{t}\geq\epsilon_{t}^{\ast}(h,\beta_{i},\theta)\).Footnote 11 In the Appendix, we derive the comparative statics of the productivity threshold. We show that, holding everything else the same, it decreases with work experience and the coefficients of Mincer wage equation, while it increases with the total number of children. As a result, life-cycle employment rates unambiguously increase following a left-shift in the distribution of total number of children ever born, or an increase in the coefficients of the Mincer wage equation, (β 0,β 1,β 2). A shift in the distribution towards delay in fertility increases employment early on. However, there are two counterbalancing effects for later ages: (1) women born in 1960 are more likely to work since they have accumulated more work experience, (2) they are less likely to work since eventually they will have younger (i.e. more costly) children.
We solve the dynamic program using a standard backward induction procedure, assuming that the continuation value in period T+1 is a function of work experience, V T+1(h). Given the expression for \(\epsilon^{\ast}_{t}\), the expected utility at time t−1 is equal to:

where ϕ and Φ denote the probability density function and the normal cumulative distribution for the productivity shocks. We use the functions ϵ t and E t V t+1 to calculate the aggregate employment rates over the life-cycle in three steps. First, since women work when the productivity shock is higher than the reservation productivity, the average employment for women of type θ is equal to:
Second, we calculate the fraction of women, μ t (h,θ), of type θ who have accumulated h years of work experience at the beginning of period t. It is given by the following formulaFootnote 12:

with initial condition μ 1(0,θ)=1 and μ 1(h,θ)=0 for h>0. Finally, the aggregate employment rate of married women in period t is equal to:
where φ(θ) denotes the distribution over fertility types.
4 Calibration: 1940 birth cohort
In this section, we calibrate our model to the life-cycle facts characterizing the 1940 cohort.Footnote 13 We stress the importance of the distributions for the number and timing of births presented in the data section. Although dynamic discrete choice life-cycle models are usually estimated using maximum likelihood techniques (e.g., Eckstein and Wolpin 1989; Van der Klaauw 1996, or Francesconi 2002), the calibration yields surprisingly good results. We obtain a very tight fit not only for the entire life-cycle employment profile of the 1940 cohort, but also for the employment by number of children at various ages. We report sensitivity analysis in the Appendix.
4.1 Parameter values
-
1.
Demographics & fertility: The model period is one year. We consider women between age 20 to 60, i.e. T=41. We assume that women are fertile between age 20 to 40, so T f =21. We set the maximum number of children, f max =4, so that women can have f∈{0,1,2,3,4} children. We characterize the joint distribution φ(θ) in (9) using the distributions of number and timing of births for the 1940 cohort. Let \(\varphi_{f}^{1940}(f)\) the marginal distribution of total number of children ever born as presented in Fig. 2 of the data section and \(\varphi_{a|f}^{1940}(a)\) the conditional distribution of the age of mother at birth of first child as presented in Fig. 3. Then, the joint distribution in (9) is equal to: \(\varphi(\theta)=\varphi_{f}^{1940}(f)\varphi_{a|f}^{1940}(a)\).
-
2.
Preferences: Agents’ utility is separable between consumption and leisure and is of the constant relative risk aversion form (CRRA). The period-t utility is given by:
$$ U(c_t,l_t)=\frac{(c_t)^{1-\sigma_c}-1}{1-\sigma_c}+A\frac {(l_t)^{1-\sigma_l}-1}{1-\sigma_l} $$(10)for all values of σ c and σ l different from 1 and
$$ U(c_t,l_t)=\ln(c_t)+A \ln(l_t) $$(11)when σ c =σ l =1. A is a positive constant. Following Keane and Wolpin (2001) and Imai and Keane (2004), we set σ c =0.52, which implies a high value for the intertemporal elasticity of substitution in consumption (IESC) compared to previous studies.Footnote 14 They find that the introduction of borrowing constraints in life-cycle models significantly increase the value for IESC. We set σ l =1. This implies a Frisch elasticity of labor supply for women with zero children of \(\frac {1}{\sigma_{l}}\frac{l_{t}}{t_{w}}=\frac{0.64}{0.36}=1.78\) and lower values for those with children (where leisure is decreased due to the time cost of children). These values are in line with estimates from Heathcote et al. (2010)Footnote 15 who use a similar model, albeit with intensive margin labor supply decisions. Sensitivity analysis shows that the model predictions crucially depend on the value of σ c and σ l .
-
3.
Costs of children: The goods and time cost of children functions, g(f,a,e s ) and t(f,a,e s ), are given by:
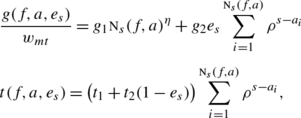 (12)
(12)with (g 1,g 2,t 1,t 2,ρ,η)∈(0,1)6, where n s (f,a) denotes the number of costly children in the household at time s and a i =a+2(i−1) denotes the age of the ith child. Notice that the goods cost of children is expressed as a fraction of husband’s income and includes a base cost, g 1, and an additional cost, g 2, when women work. We interpret the latter as market child-care costs that arise when women work and have to find someone else to look after their child. We experiment on this parameter in relation to Attanasio et al. (2008).
Since η<1, there are economies of scale in the goods cost of children. Similarly, the time cost of children includes a base cost, t 1 as well as an additional cost, t 2, when women do not work. Following Hotz and Miller (1988), we assume that the time costs of children decreases at rate, ρ<1, when children grow. Finally, we assume that children are costly until age 13.
We use evidence and estimates from the microeconometrics literature to calibrate the parameters for the costs of children: (g 1,g 2,t 1,t 2,ρ,η). Our main reference is Hotz and Miller (1988) who use a structural life-cycle model to estimate the time and goods of children. First, they find that the time cost of children decreases at rate 0.89 with age of children. Accordingly, we fix ρ=0.89. Second, we set g 1=0.09 and g 2=0.07. This is in the upper range of Hotz and Miller estimates, who find that the goods cost per child per week ranges from 11 to 17 percent of husband’s income.Footnote 16 Third, we fix t 1=0.10 and t 2=0.06, which compares well to their estimates. They find that the time cost of a newborn is about 13 percent of a woman’s time after sleeping and eating hours have been subtracted.Footnote 17 Finally, Lazear and Michael (1980) find large economies of scale, while Espenshade (1984) find that they are of the order of five percent for an additional child. We take an intermediate stand and fix η=0.92.
-
4.
Discount factor: We set δ=0.96 to match an annual interest rate of roughly 4 %.
-
5.
Male wages: We calculate the average weekly wage by age for married men born in 1940.Footnote 18 Assuming that men participate in labor markets in all period with probability one, we fit the average observed wage of men over the life-cycle using a polynomial equation of degree 4:
 (13)
(13)We find the following parameters values: β 0m =5.7083, β 1m =0.0805, β 2m =−0.0042, β 3m =0.0001, β 4m =−9.4218e −7.
-
6.
Workweek length: From time-use data (see Juster and Stafford 1991), people use on average 8 hours a day for sleeping and 2 for eating which leaves 98 hours per week to devote to work, leisure,… . From CPS data, the average workweek length for married women (conditional on being employed) is 35 hours a week. Therefore, t w =35/98=0.36 (see Greenwood et al. 2005).
-
7.
Women’s wages, terminal condition, and marginal utility of leisure: We assume that the continuation value function in period T+1 depends on work experience and is of the following form: \({V}_{T+1}(h)=a_{1}h^{a_{2}}\) with a 1>0 and a 2>0.
For women’s wages, we first use Guvenen (2005)’s estimates for the variance of the productivity shocks and fix \(\sigma^{2}_{\epsilon}=0.061\). Second, due to non-random selection of married women into the labor market, the wage coefficients of the Mincer equation, (β 0,β 1,β 2), are potentially biased.
To address this problem, we choose women’s wage coefficients, marginal utility of leisure, and parameters for the continuation value, i.e. ψ={β 0,β 1,β 2,A,a 1,a 2}, to minimize the squared deviation between the life-cycle employment rates from the model, \(\{P_{t}(\psi;\xi)\}_{t=24}^{50}\), and their data counterpart for the 1940 cohort, \(\{P^{d,1940}_{t}\}_{t=24}^{50}\):
$$ \textsc{Q}^c\bigl(\psi;\xi^c\bigr)=\sum _{t} \varPhi^{-1}_{t,t} \bigl(P_{t}\bigl(\psi;\xi^c\bigr)-P^{d,1940}_{t} \bigr)^2 $$(14)where the elements of the weighting matrix, Φ −1, are equal to the variance of participation rates over the life-cycle on the diagonal and zero otherwise. The vector of calibrated parameters, ξ c, is equal to: \(\xi^{c}=\{\{\varphi_{f}^{1940}\}, \{\varphi_{a|f}^{1940}\},\sigma_{c},\sigma _{l},g_{1},g_{2},t_{1},t_{2},\rho,\eta,\delta, \{\beta_{i}^{m}\}, t_{w},\sigma_{\epsilon}\}\).Footnote 19
Notice that the system in equation (14) is over-identified since we have 27 moments to determine 6 parameters. As a result, we cannot match all the moments perfectly. However, the fit between moments and data is good as the minimum distance for the quadratic form is equal to 0.01, i.e. Q c(ψ c;ξ c)=0.01 (see Table 3). We find that β 0=5.3117, β 1=0.0105, and β 2=−2.04e −4. Previous studies also find the sign of β 1 and β 2 to be positive and negative. However, our estimates are smaller than estimates from traditional Mincer regressions.Footnote 20 Finally, A=21.65, a 1=1.19 and a 2=0.44.
Table 3 Calibrated wage parameters
4.2 Cohort 1940: model versus data
In this section, we compare the model predictions versus data for calibrated moments as well as non-fitted moments. We first address participation and experience related predictions. Second, we discuss wage predictions.
4.2.1 Participation and experience
The calibrated life-cycle employment profile is quite close to the data (see Fig. 6). We also explore other predictions of the model for moments that we did not calibrate directly.
First, the model slightly over-predicts employment by number of children at age 30, while the fit is almost perfect at age 40 (see Figs. 7 and 8, respectively).
Second, since employment rates decrease with the number of children, women with fewer children tend to accumulate a greater number of years of work experience (see Fig. 9). At age 20, women start with no work experience. By age 50, the experience gap between women who have no children and those who have 4+ children is greater than 11 years of work experience. All of the above findings suggest that shifts in the distribution of completed fertility (total number of children ever born in a life-time) as shown in Fig. 2 in the data section potentially account for a large part of the increase in participation across cohorts. We quantify this statement in the next section.
4.2.2 Wages
We next address the model’s predictions for the average observed wage over the life-cycle (see Fig. 10) and the average observed wage by total number of children ever born at age 40 (see Fig. 11).Footnote 21 Although we match the average wage over the life-cycle, the model overstates wages at early ages and fails to capture the increase in wages at later ages. Qualitatively, wages at age 40 decrease with the number of children. Quantitatively, however, children have a much smaller impact on wages than in the data.
We discuss these patterns in three points. First, we explain in what sense the fit is actually surprisingly good. Second, we explain the selection mechanism in our model that leads to the simulated wage pattern. Third, we discuss how introducing fixed effects could provide a better fit—but at a cost.
First, wages are not a target in the calibration. Therefore, we would not expect them to be matched perfectly. Now, one important feature that is captured by our simulation is that average wages of married women by far do not grow as much as men’s or single women’s wages. In particular, as can be seen in Fig. 10, there is no growth in average wages until age 40. In fact, our mechanism dampens average wage growth so much that the overall pattern is slightly decreasing in the model as opposed to slightly increasing in the data.
Second, Fig. 12 shows model predicted wages by fertility type (0,1,2,3 or 4+). Note that we cannot plot the data counterpart to this since the CPS is not a panel data set and the researcher cannot observe how many children a woman will end up with. It is an instructive figure to understand where the average wage pattern comes from, however. As can be seen, women who know they will have 0 children over their lifetime, don’t expect to ever drop out of the labor force for reasons other than wage shocks. Hence they behave very much like men in standard life-cycle labor supply models and their wages grow over the life-cycle. For women who expect to have 4 or more children, they also tend to have them early. Therefore, there is little incentive for them to work early in life (i.e. worth giving up any more leisure than they are already giving up due to time costs of children), unless they get a really high wage shock. Hence, while participation for this type of woman is low, average accepted wages are high. This effect is decreasing in the number of children the woman expects to have over her lifetime. It is this kind of selection, that drives the average wage up during childbearing ages. As the life-cycle goes on, more and more women with many children join the labor force (as the marginal value of their leisure falls due to falling time costs of children). These women have very little experience, however, and hence low wages. By age 40, the wages are decreasing by number of children but only ever so slightly as can be seen in Fig. 11.Footnote 22
Third, our formulation misses out on an important dimension, namely that higher ability women (e.g., college educated women) tend to have children later and to have fewer. One way to account for this fact is to introduce fixed effects as an additional source of heterogeneity (i.e., market ability, \(\beta_{0}^{i}\)) and to allow for market ability to be positively correlated with age at birth of first child (which itself is negatively correlated with number of children). In such a model we find that the higher the correlation between market ability and age at birth of first child, the faster average wages fall as the number of children increases (addressing the problem in Fig. 11). The drawback of introducing fixed effects, however, is that changes in the distribution of ability types (i.e., wage levels) also change fertility related distributions, and vice versa. Hence counterfactual experiments such as those we perform in Sect. 5 are hard to interpret and call for arbitrary adjustments, unless independence is assumed. But under independence the aforementioned additional effect disappears. We therefore chose to use only one ability type, implicitly assuming independence.Footnote 23
5 Experiments: 1960 cohort
Three influential papers have stressed the importance of changes in the pure gender wage gap (Jones et al. 2003), changes in returns to experience (Olivetti 2006), and changes in child-care costs relative to life-time earnings (Attanasio et al. 2008) to account for changes in women’s labor supply either over time or across cohorts. In this section, we assess the quantitative importance of these 3 forces as follows.
Taking changes in fertility patterns into account, we use our model to quantify what changes in women’s wages and child-care cost are needed to match the life-cycle participation choices of women born in 1960. Using distributions for number and timing of births of the 1960 cohort, we choose the pure gender wage gap, β 0 (relative to β 0m ), the returns to experience, β 1,β 2, and the cost of child-care, g 2, to match the life-cycle employment rates of the 1960 cohort, holding all other calibrated parameters constant. We set the vector, ψ={β 0,β 1,β 2,g 2}, to minimize the following quadratic form:
where \(\xi^{e}=\{\{\varphi_{f}^{1960}\},\{\varphi_{a|f}^{1960}\}, \sigma_{c},\sigma_{l},A,g_{1},t_{1},t_{2},\rho,\eta,\delta, \{\beta_{i}^{m}\} ,t_{w},\sigma_{\epsilon},a_{1},a_{2}\}\).
Let ψ e=argmin ψ∈Ψ Q e(ψ;ξ e), the solution to the above system. This exercise allows us to answer questions such as: taking into account changes in fertility patterns, by how much do the coefficients of women’s Mincer wage equation and child-care cost need to change to explain the observed patterns in women’s employment?
Our model has the same qualitative predictions as in Jones et al. (2003), Olivetti (2006), or Attanasio et al. (2008). The pure gender wage gap and the child-care cost decrease, while returns to experience increase across cohorts in order to match changes in women’s employment across cohorts (see Table 4). Quantitatively, the pure gender wage gap decreases, i.e. β 0 increases by less than 1 percent, returns to experience increase as the coefficient on experience, β 1, and experience squared, β 2, increase by 42 percent and 21 percent, respectively, and finally the price of child-care, g 2, decreases by 18.5 percent. We compare these findings to the literature below.
The fit for life-cycle employment profile of the 1960 cohort following changes in wage and fertility is good (see Fig. 13). Since the increase in participation rates occurs mainly for women with 1 and 2 children, the experience gap between women with 0 and 1 child is less than 1.5 years at age 43 compared to more than 5 years for women born in 1940 (see Fig. 16). Finally, employment at age 30 increases the most for women with 1 and 2 children and we overshoot for participation of women with 0 and 1 child at age 40 (see Figs. 14 and 15).
Since we implicitly assumed that changes in fertility patterns, gender wage differentials, and cost of child-care account for 100-percent of changes in women’s employment across cohorts, we perform a decomposition exercise to assess their relative (quantitative) importance. We write:
where changes in fertility include changes in number and timing of births, changes in wages include changes in the pure gender wage gap and returns to experience, and R is a residual term to account for potential interaction between all the variables. We present the results of the decomposition exercise for various age groups in Fig. 17 and Table 5. In each experiment, we change some parameters to their 1960-cohort values, holding all other parameters at their 1940-cohort values. That is, for A.Fertility, we change both the distributions of level and timing of births as per Figs. 2 and 3, holding β 0,β 1,β 2 and g 2 at their 1940-cohort values. This experiment is further decomposed into a.Number holding β 0,β 1,β 2 and g 2 as well as timing of births at their 1940-cohort values and b.Timing holding β 0,β 1,β 2 and g 2 as well as number of children at their 1940-cohort values. For B.Wages, we change β 0,β 1 and β 2 to their 1960-cohort values holding g 2 as well as number and timing of births at their 1940-cohort values. This experiment is further decomposed into a.Pure wage gap where only β 0 is changed to its 1960-cohort value and b.Returns to experience where only β 1 and β 2 are changed to their 1960-cohort values. Finally, for C.Child-Care Cost we change g 2 to its 1960-cohort value holding β 0,β 1 and β 2 as well as number and timing of births at their 1940-cohort values. The residual is then calculated from (16).
In order of importance, we find that changes in women’s wages account for 68 percent of changes in women’s employment across cohorts, followed by changes in child-care cost (21 percent), fertility (9 percent), and the residual term (2 percent).
More precisely, we can compare our results to the literature as follows. First, our implied decrease in the pure gender wage gap is an order of magnitude smaller than the (lifetime) pure gender wage gap implied by Jones et al. (2003), namely 2.1 percentFootnote 24 versus 27 percent. This may be due to the fact that they don’t take the lifecycle experience effect of children into account. That is, if that was taken into account, the needed change in the gender wage gap to generate the increase in the observed wage—a function of accumulated human capital in Jones et al. (2003)’s model—would be much smaller. Their change in the gender wage gap accounts for almost the entire change in married female hours worked, while our (much smaller) change accounts for only 6 percent of the change observed in the data.
Second, the implied change in the marginal return to experience at age 23 between the 1940 and 1960 cohorts (i.e. from the year 1963 to the year 1983) is about 40 percentFootnote 25 while Olivetti (2006) finds that the marginal return to experience at age 20 between the 1970s and 1990s increased by only 25 percent. This difference could be explained by the fact that Olivetti’s estimates are obtained using all ages of women at each point in time, while our measures are cohort-specific. While Olivetti finds that changes in returns to experience account for 96 percent of the change observed in the data, we find that they account for only 62 percent despite the larger exogenous change. This difference in findings may be due to the fact that Olivetti uses the intensive margin of hours worked, while we consider the extensive margin.
Third, Attanasio et al. (2008) find that child care costs decreased by 5 percent to 20 percent while our estimate implies a decrease of 18.5 percent.Footnote 26 A decrease of 20 percent in their model can account for slightly more than half of the increase in female labor force participation, while in our model changes in the price of child-care alone account for only 21 percent of the change observed in the data.
Finally, we find that changes in fertility patterns have the largest impact for the age group 20–35 and changes in the number and timing of births offset one another. Finally, changes in fertility patterns also affect changes in women’s life-cycle employment in an indirect way through their interaction with changes in women’s wages and cost of child-care.
6 Concluding remarks
We have presented data on employment and fertility for cohorts of married women born between 1940 and 1960. Using a life-cycle model of married female employment with experience accumulation, our analysis shows the following. First, fertility patterns (total number of children ever born and age of mother at birth of first child) are crucial determinants of the life-cycle employment profile for married women. Second, changes in gender wage differentials and costs of children needed to account for changes in women’s life-cycle employment are smaller than previously found in the literature once we take into account changes in fertility patterns. Third, changes in women’s wages (in particular, returns to experience) have the largest impact on women’s employment decisions.
One open question is: What caused the decrease and delay in fertility? Our current work in progress is to endogenize fertility and timing of births decisions to ask whether changes in wages can also account for the delay in fertility. Preliminary results show that the delay, though positive, is largely left unaccounted for. Something else seems to have caused the delay in fertility. Several related questions come to mind: How is fertility related to the marriage decision? Was the change in fertility decisions simply due to cultural changes and changes in social norms? In what sense and can we attempt to measure these changes? The answers to these questions are closely intermingled and hard to disentangle from the question about why women tend to have children later and take care of them differently than they used to. They are however crucial to set up a useful model of fertility choices in terms of number and timing of births as well as child-care arrangements.
The other open question is why wage levels and returns to experience changed more for women than they did for men. Besides straight out discrimination, many other more readily quantifiable hypotheses can be considered. Changing occupational opportunities due to the rise in the service sector, changing educational investments pertaining more to women than men because of initial conditions are only a few avenues to be explored further.
Executive summary
In the United States, as well as in many other developed countries, life-cycle employment profiles of married women born around mid-century changed in a noticeable way. Employment rates of women born in 1940 and earlier are low at childbearing ages (between age 20 to 35) and increase over the life-cycle. Changes in employment across cohorts are not uniform along the life-cycle, however. They are very pronounced at childbearing ages and more modest at later ages. As a result, life-cycle employment profiles of women born in 1960 not only shift upwards but also become much flatter.
In this paper, we build a dynamic life-cycle model of employment decisions of married women to assess the quantitative importance of three competing explanations of the change in life-cycle employment profiles: the decrease and delay in fertility, the increase in relative wages of women to men, and the decline in child-care costs. The incentives at work are as follows. First, because child-rearing is intensive in women’s time, employment at childbearing ages increases as fertility is reduced. Second, postponing fertility allows women to reach childbearing ages with a higher stock of accumulated work experience, thereby increasing their incentives to remain employed when having children. Finally, either an increase in women’s wages relative to men or a decline in the cost of child-care makes working more attractive at childbearing ages, which feeds back on employment decisions later on in life because of experience accumulation.
After choosing the parameters of the model to replicate the life-cycle facts observed characterizing the 1940 cohort, we show that the decrease and delay in fertility and the decline in child-care cost affect employment very early in life, while increases in relative wages affect employment increasingly with age. Assuming that the three forces account for 100 percent of the shift in life-cycle employment profiles, we find that changes in women’s wages (in particular, returns to experience) account for 67 percent of the increase, versus 21 percent for cost of child-care, and 9 percent for fertility patterns (the residual term is equal to 3 percent).
The contribution of our accounting exercise is clear. Three influential papers have stressed the importance of changes in the pure gender wage gap (Jones et al. 2003), changes in returns to experience (Olivetti 2006), and changes in child-care costs relative to life-time earnings (Attanasio et al. 2008) to account for changes in women’s labor supply either over time or across cohorts. Since our model nests these three potential explanations and adds another one (the decrease and delay in fertility), we can assess the quantitative importance of each of these forces separately.
We find that they affect employment of women in distinct age groups differently and that changes in returns to experience have the largest impact on women’s employment. Moreover, we show that a careful modeling of the distributions for number and timing of births is fruitful. First, it allows us to match the entire life-cycle employment of married women born in 1940. Second, once we control for changes in fertility patterns, exogenous changes in women’s wages and cost of children that are needed to replicate changes in employment across cohorts are smaller in magnitude or larger but with a smaller effect on female labor supply compared to the ones found in Jones et al. (2003) for the gender wage gap, Olivetti (2006) for returns to experience, and Attanasio et al. (2008) for decreases in the cost of child-care.
Numerous other explanations for the increase in employment of married women, either over time or across cohorts, have been proposed. These include falling prices of home appliances (Greenwood et al. 2005), changes in the perceived value of marriage (Caucutt et al. 2002), the introduction of the pill (Goldin and Katz 2002), changes in social norms (Fernandez et al. 2004), tax reform (Bar and Leukhina 2009), or gender-biased technological change favoring women (Galor and Weil 1996), to name only a few. These papers are certainly important. However, it is virtually impossible, let alone desirable, to include all of the aforementioned forces into one single model. To perform our accounting exercise, we chose the ones which seemed the most likely to influence women’s employment decisions at childbearing ages.
Kurzfassung
In den USA und vielen anderen Industrieländern haben sich die Lebensverlauf-Beschäftigungsprofile verheirateter Frauen, die um die Mitte des Jahrhunderts geboren wurden, bemerkenswert verändert. Erwerbstätigenquoten von Frauen der Jahrgänge 1940 und früher sind im gebärfähigen Alter (zwischen 20 und 35) niedrig und steigen im weiteren Lebensverlauf. Erwerbstätigkeitsveränderungen über Kohorten sind jedoch im Lebensverlauf nicht einheitlich. Sie sind im gebärfähigen Alter sehr ausgeprägt und in späteren Jahren geringer. Im Ergebnis verschieben sich Lebensverlauf-Beschäftigungsprofile von Frauen des Jahrgangs 1960 nicht nur nach oben sondern werden auch viel flacher.
In dieser Abhandlung konstruieren wir ein dynamisches Lebenszyklusmodell von Beschäftigungsentscheidungen verheirateter Frauen, um die quantitative Bedeutung dreier konkurrierender Erklärungen für veränderte Beschäftigungsprofile im Lebensverlauf einzuschätzen: Geburtenrückgang und später eintretende Geburten, Zunahme relativer Löhne von Frauen zu Männern und gesunkene Kosten für Kinderbetreuung. Die Anreize wirken wie folgt: Erstens steigen die Beschäftigungszahlen im gebärfähigen Alter an, sobald die Geburtenzahlen zurückgehen, da es Frauen viel Zeit kostet, Kinder aufzuziehen. Zweitens erlauben spätere Geburten es den Frauen, bis dahin mehr Arbeitserfahrung anzusammeln und steigern somit die Anreize, auch als Mutter berufstätig zu bleiben. Letztlich machen entweder der Anstieg der relativen Löhne von Frauen zu Männern oder gesunkene Kosten für Kinderbetreuung Beschäftigung im gebärfähigen Alter attraktiver, was Beschäftigungsentscheidungen im späteren Leben aufgrund der Ansammlung von Erfahrungen beeinflusst.
Nach Auswahl der Modellparameter zur Replikation der Lebenszyklus-Fakten, welche die 1940er Kohorte charakterisieren, zeigen wir, dass der Geburtenrückgang und später eintretende Geburten und gesunkene Kosten für Kinderbetreuung Beschäftigung sehr früh im Leben beeinflussen, während Anstiege relativer Löhne Beschäftigung im Alter stärker beeinflussen. Unter der Annahme, dass die drei Einflüsse 100 Prozent der Verschiebung der Lebensverlauf-Beschäftigungsprofile ausmachen, stellen wir fest, dass Veränderungen der Entlohnung von Frauen (besonders Entlohnung gemäß Erfahrung) 67 Prozent des Anstiegs ausmachen, wohingegen 21 Prozent auf Kinderbetreuung und 9 Prozent auf Geburtenmuster entfallen (der Rest beträgt 3 Prozent).
Der Beitrag unserer Bilanzierung ist klar. Drei einflussreiche Abhandlungen haben die Bedeutung von Veränderungen im rein geschlechtsspezifischen Lohngefälle (Jones et al. 2003), von Veränderungen von Entlohnung gemäß Erfahrung (Olivetti 2006) und Veränderungen von Kinderbetreuungskosten im Verhältnis zu lebenslangem Einkommen (Attanasio et al. 2008) betont, um Veränderungen des Arbeitskräfteangebots von Frauen entweder über die Zeit oder über Kohorten zu begründen. Da unser Modell diese drei potenziellen Erklärungen kombiniert und eine weitere hinzufügt (Geburtenrückgang und später eintretende Geburten), können wir die quantitative Bedeutung jedes dieser Einflüsse separat einschätzen.
Wir stellen fest, dass sie die Beschäftigung von Frauen in bestimmten Altersgruppen unterschiedlich beeinflussen und dass Veränderungen der Entlohnung gemäß Erfahrung den größten Einfluss auf die Beschäftigung von Frauen haben. Desweiteren zeigen wir, dass eine sorgfältige Modellierung der Verteilungen von Anzahl und Terminierung von Geburten vielversprechend ist. Erstens erlaubt uns das, die gesamten Lebensverlauf-Beschäftigungsprofile verheirateter Frauen des Jahrgangs 1940 abzugleichen. Zweitens sind, sobald wir Veränderungen in Geburtenmustern, exogene Veränderungen der Entlohnung von Frauen und Kosten für Kinder kontrollieren, die zur Replikation benötigt werden, Beschäftigungsveränderungen über Kohorten kleiner oder größer im Ausmaß, aber mit einer geringeren Auswirkung auf das Arbeitskräfteangebot von Frauen, verglichen mit denen, die bei Jones, Manuelli und McGrattan (2003) im geschlechtsspezifischen Lohngefälle aufzufinden sind, bei Olivetti (2006) für Entlohnung gemäß Erfahrung und bei Attanasio et al. (2008) für Rückgänge in den Kosten für Kinderbetreuung.
Man hat zahlreiche andere Erklärungen für den Anstieg der Beschäftigung verheirateter Frauen entweder über Zeit oder über Kohorten vorgeschlagen. Diese beinhalten sinkende Preise für Haushaltsgeräte (Greenwood et al. 2005), Veränderungen im wahrgenommenen Wert der Ehe (Caucutt et al. 2002), die Einführung der Pille (Goldin and Katz 2002), Veränderungen sozialer Normen (Fernandez et al. 2004), die Steuerreform (Bar and Leukhina 2009) oder geschlechtsbezogene technologische Veränderungen zum Vorteil von Frauen (Galor and Weil 1996), um nur einige zu nennen. Ohne Zweifel sind diese Abhandlungen von Bedeutung. Es ist jedoch nahezu unmöglich, geschweige denn wünschenswert, alle vorgenannten Einflüsse in ein einziges Modell aufzunehmen. Für unsere Bilanzierung wählen wir diejenigen, die am wahrscheinlichsten Beschäftigungsentscheidungen von Frauen im Gebäralter beeinflussen.
Notes
All raw data was downloaded from the Integrated Public Use Micro-data Series (IPUMS) available at http://www.ipums.org.
We assume that women are no longer fertile after age 40 and present employment by number of children ever born rather than employment by number of children in the household.
Heckman et al. (2003) find that the strongest effect of wages and costs of children operate through the time of the first birth.
Since changes in women’s labor supply across cohorts mainly occur at the extensive margin, this assumption is fine as a starting point. However, recent work by Erosa et al. (2005) shows that, among working women, those who have children work fewer hours than the ones without children. Alternatively, Francesconi (2002) proposes a life-cycle model of women’s labor supply and fertility where women can choose between working part-time or full-time. He finds that mothers prefer to interrupt their careers for a short time around childbirth rather than working on a part-time basis.
We further discuss the i.i.d. assumption below.
Attanasio et al. (2008) study a life-cycle model of women’s employment with borrowing and savings. They show that the elasticity of women’s employment increases once savings and borrowing are allowed.
Note that, if the woman works every period, work experience coincides with age and (2) boils down to a simple Mincer equation.
Note that, because of the i.i.d. assumption, the contemporaneous productivity shock enters the expression in (5) only once, through the woman’s wage offer.
The law of motion for μ is given by: μ t+1(h,θ)=μ t (h,θ)(1−p t (h,θ)) for women who have no prior work experience, i.e. h=0. On the other hand, it is equal to μ t+1(h,θ)=μ t (h−1,θ)p t (h−1,θ) for women who have worked in all periods, i.e. h=t.
With CRRA utility, the intertemporal elasticity of substitution in consumption (IESC) is equal to the inverse of the coefficient of risk aversion, σ c (see Kimball 1990). Hubbard et al. (1994) survey the literature on life-cycle consumption, savings, and wealth accumulation and conclude that a conventional value for σ c is equal to 3, which implies a value for IESC of \(\frac{1}{3}\). They do not consider, however, imperfection in capital markets.
See page 702, footnote 22.
Note that it is very common to find wide ranges of goods cost estimates in the literature. See also Bernal (2004) who finds a comparable wide range for child-care expenditures.
Hill and Stafford (1980) analyzing time use data in 1976 find that women spend 550 minutes per child per week in child-care if they have one preschooler and 440 minutes per child per week if they have two (p. 237). This corresponds to about 10 percent of a woman’s total time after sleeping and eating hours have been subtracted. However, housework time can to some extent be viewed as time spent where watching children is possible at the same time.
The Current Population Survey (CPS) provides individual data on total labor income earned in the previous calendar year as well as weeks worked last year. Weekly wages are then total labor income divided by weeks worked.
We use the downhill simplex method to solve for the optimal vector, ψ c=argmin ψ∈Ψ Q c(ψ;ξ c), which requires only function evaluations, not derivatives, and is efficient when the size of the simplex is small (see Nelder and Mead 1965).
This result is consistent with the findings of Eckstein and Wolpin (1989), who show that simple wage regressions on female wages yield biased estimates because of non-random selection in labor markets and experience accumulation. They find that, when using a structural model of women’s employment decisions, the coefficient on experience and experience squared in the Mincer equation, β 1 and β 2, are equal to 0.0241 and −2.4e −4, respectively, compared to 0.037 and −5e −4 in simple wage regressions.
We normalize wages by number of children by the wage of women with 0 children.
A similar selection problem exists in Attanasio et al. (2008) and hence, the same problem of matching the wage pattern (compare Figs. 8 and 12).
Introducing fixed effects becomes useful in a model with endogenous fertility, where high ability women choose to have fewer children and to have them later. As a result, a change in wages (or the distribution of abilities) will affect both, fertility choices and participation decisions, and no arbitrary adjustments are needed. This is the object of work in progress by the authors.
The parameter β 0 increases from 5.3117 to 5.3217. The relative wage of women to men at age 20 therefore changes from \(\frac {e^{5.3117}}{e^{5.7083}}=0.6726\) to 0.6794. Hence, the change in the pure gender wage gap is \(\frac{0.3206-0.3274}{0.3274}=-0.021\).
The parameter β 1 increased from 0.0105 to 0.0149. Since the effect of β 2 is negligibly small early in life, the percentage change is \(\frac {0.0149-0.0105}{0.0105}=0.42\)
The parameter g 2 decreased from 0.07 to 0.057. Hence, we get \(\frac{0.057-0.07}{0.07}=-0.185\).
For very high values of g 1 relative to g 2, the marginal utility of consumption for women with children is so high that employment rates increases with the number of children, which is counterfactual.
References
Altug, S., Miller, R.A.: The effect of work experience on female wages and labor supply. Rev. Econ. Stud. 65(1), 45–85 (1998)
Attanasio, O., Low, H., Sanchez-Marcos, V.: Explaining changes in female labor supply in a life-cycle model. Am. Econ. Rev. 98(4), 1517–1552 (2008)
Bar, M., Leukhina, O.: To work or not to work: did tax reforms affect labor force participation of married couples? B.E. J. Macroecon. 9(1), 28 (2009)
Bernal, R.: The effect of maternal employment and child care on children’s cognitive development. Working Paper, Northwestern University (2004)
Caucutt, E.M., Guner, N., Knowles, J.: Why do women wait? Matching, wage inequality, and the incentives for fertility delay. Rev. Econ. Dyn. 5(4), 815–855 (2002)
Eckstein, Z., van der Berg, G.J.: Empirical labor search: a survey. J. Econom. 136(2), 531–564 (2007)
Eckstein, Z., Wolpin, K.I.: Dynamic labour force participation of married women and endogenous work experience. Rev. Econ. Stud. 56(3), 375–390 (1989)
Erosa, A., Fuster, L., Restuccia, D.: A quantitative theory of the gender wage gap in wages. Working Paper, University of Toronto (2005)
Espenshade, T.J.: Investing in Children: New Estimates of Parental Expenditures. Urban Institute Press, Washington (1984)
Fernandez, R., Fogli, A., Olivetti, C.: Preference formation and the rise of women’s labor force participation: evidence from WWII. NBER Working paper 10589, National Bureau of Economic Research (2004)
Francesconi, M.: A joint dynamic model of fertility and work of married women. J. Labor Econ. 20(2), 336–380 (2002)
Galor, O., Weil, D.N.: The gender gap, fertility and growth. Am. Econ. Rev. 86(3), 374–387 (1996)
Goldin, C., Katz, L.F.: The power of the pill: oral contraceptives and women’s career and marriage decisions. J. Polit. Econ. 110(4), 730–770 (2002)
Greenwood, J., Seshadri, A., Yorukoglu, M.: Engines of liberation. Rev. Econ. Stud. 72(1), 109–133 (2005)
Guvenen, F.: Learning your income: are labor income shocks really very persistent? Working paper, University of Rochester (2005)
Hansen, L.P., Heckman, J.J.: The empirical foundations of calibration. J. Econ. Perspect. 10(1), 87–104 (1996)
Heathcote, J., Storesletten, K., Violante, G.L.: The macroeconomic implications of rising wage inequality in the united states. J. Polit. Econ. 118(4), 681–722 (2010)
Heckman, J.J., Lochner, L.J., Todd, P.E.: Fifty years of mincer earnings regressions. Working paper 9732, National Bureau of Economic Research (2003)
Heckman, J.J., Walker, J.R.: The relationship between wages and income and the timing and spacing of births: evidence from Swedish longitudinal data. Econometrica 58(6), 1411–1441 (1990)
Hill, R.C., Stafford, F.P.: Parental care of children: time diaries estimates of quantity, predictability, and variety. J. Hum. Resour. 15(2), 220–239 (1980)
Hotz, J.V., Miller, R.A.: An empirical analysis of life cycle fertility and female labor supply. Econometrica 56(1), 91–118 (1988)
Hubbard, G.R., Skinner, J., Zeldes, S.P.: The importance of precautionary motives in explaining individual and aggregate saving. Carnegie-Rochester Conf. Ser. Public Policy 40, 59–125 (1994)
Imai, S., Keane, M.P.: Intertemporal labor supply and human capital accumulation. Int. Econ. Rev. 45(2), 601–641 (2004)
Jones, L.E., Manuelli, R., McGrattan, E.S.: Why are married women working so much? Federal Reserve Bank of Minneapolis Staff report. (May 2003)
Juster, T.F., Stafford, F.P.: The allocation of time: empirical findings, behavioral models, and problems of measurement. J. Econ. Lit. 29(2), 471–522 (1991)
Keane, M.P., Wolpin, K.I.: The effect of parental transfers and borrowing constraints on educational attainment. Int. Econ. Rev. 42(4), 1051–1103 (2001)
Kimball, M.S.: Precautionary saving in the small and in the large. Econometrica 58(1), 53–73 (1990)
Kydland, F.E., Prescott, E.C.: Time to build and aggregate fluctuations. Econometrica 50(6), 1345–1370 (1982)
Lazear, E.P., Michael, R.T.: Family size and the distribution of real per capita income. Am. Econ. Rev. 70(1), 91–107 (1980)
Meghir, C., Pistaferri, L.: Income variance dynamics and heterogeneity. Econometrica 72(1), 1–32 (2004)
Nelder, J.A., Mead, R.: A simplex method for function minimization. Comput. J. 7, 308–313 (1965)
Olivetti, C.: Changes in women’s hours of work: the effect of changing returns to experience. Rev. Econ. Dyn. 9, 557–587 (2006)
Prescott, E.C.: Theory ahead of business cycle measurement. Q. Rev. - Fed. Reserve Bank Minneap. 10, 9 (1986)
Schoonbroodt, A.: Small sample bias using maximum likelihood versus moments: the case of a simple search model of the labor market. Working paper, University of Minnesota (2002)
Sommer, K.: Fertility choice in a life cycle model with idiosyncratic uninsurable earnings risk (2012). Available at http://kamilasommer.net
Van der Klaauw, W.: Female labour supply and marital status decisions: a life-cycle model. Rev. Econ. Stud. 63(2), 199–235 (1996)
Author information
Authors and Affiliations
Corresponding author
Additional information
All errors are ours.
Appendix
Appendix
1.1 A.1 Life-cycle patterns by education
We present data for life-cycle employment profiles and fertility by education.
1.1.1 A.1.1 Employment
Employment profiles over the life-cycle and their changes across cohorts differ considerably by education. They are mostly increasing in age for high school graduates, while college women tend to work a lot before childbearing ages, then drop out of the labor force and finally join the labor force again after childbearing ages (see Figs. 18 and 19, respectively).
However, changes in employment rates across cohorts are the largest at childbearing ages. Between age 20 and 35, employment rates increased on average by 26 and 27 percentage points for high school and college graduates respectively. Between age 36 and 50, employment only increases by 10 and 4 percentage points for HS and College graduates.
1.1.2 A.1.2 Fertility
In Table 6, we present the total number of children ever born and the average age of mother at birth of first child by education. Fertility levels decreases with education. However, changes are the largest for High School graduates women. On the other hand, age of mother at birth of first child increases with education and changes are the largest for College educated women.
1.2 A.2 Comparative statics
We derive the comparative statics of ϵ ∗ with work experience, h, coefficients of Mincer wage equation, {β i } i=0,1,2, and women’s type, θ. Consider two women of type θ who have the same number of years of work experience in period t, \(h^{A}_{t}=h^{B}_{t}\). Suppose that woman A receives a productivity shock above the reservation shock, while woman B receives a shock below. Next period, we have \(h^{A}_{t+1}=h^{B}_{t+1}+1\). This affects their respective continuation values as well as the period utility if they decide to work (since the wage is increasing in the number of years of work experience). The indirect utility both, from working and not working, is higher for woman A than woman B (see Fig. 20), but the difference in the former is larger than the difference in the latter. Hence, \(\epsilon_{t+1}^{\ast}(h^{A},\beta_{i},\theta)<\epsilon_{t+1}^{\ast }(h^{B},\beta_{i},\theta)\) and woman A is more likely to work in the future. By analogy, the same comparative statics apply for β i , holding everything else the same. Women are more likely to work, following a decrease in the gender wage gap due to an increase in β 0 or an increase in the returns to experience due to an increase in (β 1,β 2).
Next, consider two women who have a different number of children over their life-time, f A<f B, but the same age at birth of first child, a A=a B. Here comparative statics depend on the relative magnitudes of time and goods costs. For sake of intuition, consider two extreme cases. In the first case, children are costly if the woman works, while in the second, they are costly if she doesn’t work. Therefore, in case (1) (case (2)), women with fewer children are more (less) likely to work. In the data section above, we described employment by number of children in the household and found that it is decreasing. Calibrating to this fact, parameters adjust such that a version of case (1) applies. Therefore, under our parameters, the reservation shock is higher for women who have more children over their life-time. Thus, they are less likely to work. Finally, consider two women who differ in their age at birth of first child, i.e. a A>a B, but will have the same number of children over their life-time, f A=f B. Then for some periods, woman A will have fewer children than woman B. She will therefore be more likely to work, everything else the same. However, once she starts to have children herself, she will have younger children in the household than woman B. Since younger children are costlier, she is less likely to work during those periods.
1.3 A.3 Sensitivity analysis
In this section, we perform sensitivity analysis to assess the robustness of our calibrated parameters. We analyze the impact of a 10-percent change in our calibrated parameters on the goodness of fit for life-cycle participation and participation by number of children at age 30 and 40. Changing only 1 parameter at a time, we choose women’s wages coefficients, the marginal utility of leisure, and parameters for the continuation value to minimize the squared deviation between the life-cycle employment rates from the model and their data counterpart. For example, to assess the impact of a 10-percent increase in the base goods cost, g 1, we set the vector, ψ={β 0,β 1,β 2,A,a 1,a 2}, to minimize the following quadratic form:
where \(\xi^{s}(g_{1})=\{\{\varphi_{f}^{1940}\},\{\varphi_{a|f}^{1940}\},\sigma_{c}, \sigma_{l},1.1g_{1},g_{2},t_{1},t_{2}, \rho,\eta,\delta,\{\beta_{i}^{m}\} ,t_{w},\sigma_{\epsilon}\}\). Let
the solution to the above system. We calculate the percentage change (elasticity) in the coefficients of women’s wages and marginal utility of leisure as follows: \(\lambda_{\psi_{i},g_{1}}=\frac{\psi^{s}_{i}(g_{1})-\psi^{c}_{i}}{\psi^{c}_{i}}/\frac {\Delta g_{1}}{g_{1}}\). We assess the impact of a 10-percent change in parameters for preferences, cost of children, and the standard deviation of the productivity shock and present our results in Table 7.
Since the marginal utility of consumption for women with children is very high, the relationship between employment and number of children flattens out following an increase in the base goods cost of children, g 1 (relative to g 2).Footnote 27 The decrease in employment rates of women with 0 and 1 child is achieved through an increase in the marginal utility of leisure, A, and a decrease in returns to work experience, (β 1,β 2). On the other hand, when the base time cost t 1 is high relative to t 2, the marginal utility of leisure for women with children is very high. As a result, the relationship between employment and number of children becomes steeper. Finally, the goodness of fit for life-cycle employment rates is very sensitive to values of ρ, which provides strong support for the estimate of Hotz and Miller (1988).
The wage-experience profile and the marginal utility of leisure are also very sensitive to the coefficient of risk aversion, σ c and the intertemporal elasticity in labor supply, σ l , which confirms the low values for σ c in life-cycle models with borrowing constraints (see Keane and Wolpin 2001). Note that since the marginal utility of leisure decrease when σ l increases, employment by number of children flattens out. Finally, changes in the standard deviation of the productivity shocks have mild effects on the goodness of fit for life-cycle participation and participation by number of children at age 30 and 40.
Rights and permissions
About this article
Cite this article
Buttet, S., Schoonbroodt, A. An accounting exercise for the shift in life-cycle employment profiles of married women born between 1940 and 1960. J Labour Market Res 46, 253–271 (2013). https://doi.org/10.1007/s12651-013-0130-5
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12651-013-0130-5